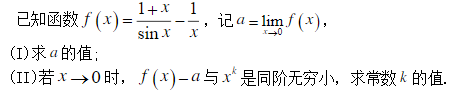证明方程 x x x 1 n n-1 + n 1的整数 ,在区间 1 ,1 2 内有且仅有一个实根; (II) 记(I) 中的实根为 xn,证明 lim n n x 存在,并求此极限

正确答案: 
本题解析: 暂无解析
已知函数 f ( x) 满足方程 f (x) f (x) 2 f (x) 0 及 ( ) ( ) 2 x f x f x e , (I) 求 f (x) 的表达式 (II) 求曲线 2 2 0 ( ) ( )d x y f x f t t 的拐点.
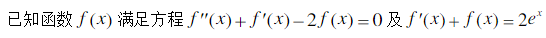
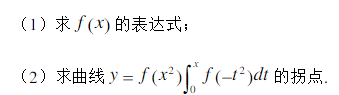
已知函数 1 1 sin x f x x x ,记 0 lim x a f x , (I) 求 a 的值 (II) 若 x 0 时, f x a 与 k x 是同阶无穷小,求常数 k 的值 .